卷积神经网络的基本概念

一、深度学习简介

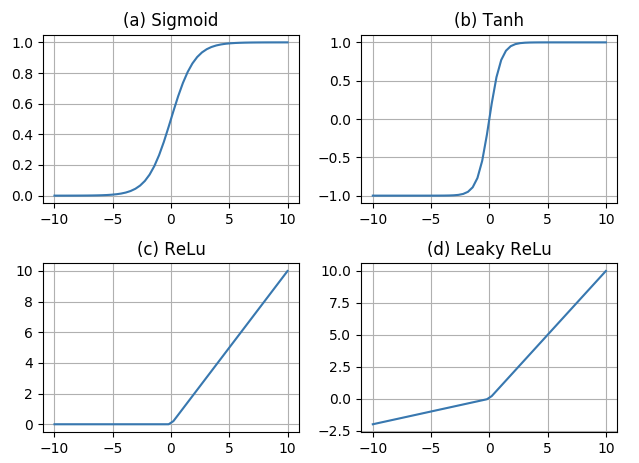
　　深度学习是机器学习的一个子领域，它使用多层非线性信息处理及抽象，用于监督和非监督的特征学习和表示、分类及模式识别。深度学习在不同的学习任务上都取得了很大的成功,特别是在Imagenet的图像分类任务和LFW的人脸识别任务上更是超过了人类水平。相比于传统方法，深度学习具有很多优势。首先深度学习通用性更强，而传统方法针对不同的任务需要设计不同的特征。深度学习相较于传统方法可以自动从原始数据中提取特征，所以同个算法可以应用到各种类似的任务中来，比如目标检测任务，它可以同时用于人脸检测，行人检测，一般物体检测任务上。其次深度学习学习的特征具有很强的迁移能力，比如它在ImagetNet分类任务上学习的特征，在目标检测任务上也可以获得非常好的效果。最后一个优势是它的工程开发、优化、维护成本较低。深度学习计算主要是卷积和矩阵乘，针对这种计算优化，所有的深度学习算法都可以提升性能；另外，通过组合现有的层，我们可以实现大量复杂网络结构和算法，开发维护成本也很低。随着深度学习的发展，当前也存在着很多种不同类型的网络体系结构，如深度自编码网络、卷积神经网络、时间递归神经网络等。其中应用最广泛的是卷积神经网络。

二、卷积神经网络的发展过程

　　卷积神经网络是一种深度学习网络结构，它的发明灵感来自于生物的自然视觉感知机制。在1990年，LeCun等人$^{[1]}$发表了开创性的论文建立了CNN的现代框架，并随后提出了对它的改进$^{[2]}$。他们开发了一个多层的人工神经网络叫做LeNet-5，用于识别手写体数字图片。与其它神经网络类似，LeNet-5具有多个网络层，并且可以通过反向传播算法$^{[3]}$来训练。它可以从输入图片中学习到有效的表示，这也让它可以直接通过原图来进行识别，而不需要先对图片提取特征。但是由于当时缺少大规模的训练数据以及受到计算能力的限制，他们的网络在更复杂的问题上(如大规模的图片和视频分类任务)无法表现得很好。
　　自2006年以来，很多的方法已经被开发出来用于改进卷积神经网络$^{[5-8]}$。其中最著名的是Krizhevsky等人提出的经典的CNN体系结构，AlexNet$^{[6]}$，该体系结构在图像分类任务上的性能大大超过了先前的方法，在图像分类任务上的top-1和top-5错误率分别从47.1%和28.2%降低到37.5%和17.0%。AlexNet在网络结构上与LeNet-5类似，但是网络结构比LeNet-5更加深。随着AlexNet的成功，很多的工作被提出来改进它的性能。其中，最有代表性的工作是ZFNet$^{[9]}$，VGGNet$^{[7]}$, GoogleNet$^{[8]}$,和ResNet$^{[10]}$。随着更多改进方法的提出，当前卷积神经网络在很多任务上都获得很高的性能，并且在某些任务中超过了人类水平。

三、卷积神经网络的基本部件及训练方法简介　

　　我们将输入数据输入到网络中，并经过卷积层、池化层、全连接层，最后到达输出层输出结果的过程称为前向传播。前向传播得到的估计值通常与实际结果会有误差，模型的训练过程就是不断缩小估计值与实际值之间的误差的过程。在这个过程中我们利用损失函数来衡量估计值和实际结果的误差带来的损失，并试图让该损失尽可能小，为此我们将误差带来的损失从输出层向隐含层传播，直至传播到输入层，这个过程称为反向传播。在传播过程中通过某种误差调整策略，如随机梯度下降，调整模型参数，使得模型误差减小。整个模型的训练过程就是不断迭代前向传播，反向传播并调整模型参数这个过程，直至最后模型收敛。在模型收敛之后，模型的每次预测过程就是一次前向传播过程。虽然当前存在很多不同的卷积神经网络体系结构，但是它们的基本部件是很相似的。如LeNet-5，它主要包含3种部件，卷积层、池化层和全连接层。下面给出了卷积神经网络的各个部件及其训练方法的简单介绍。

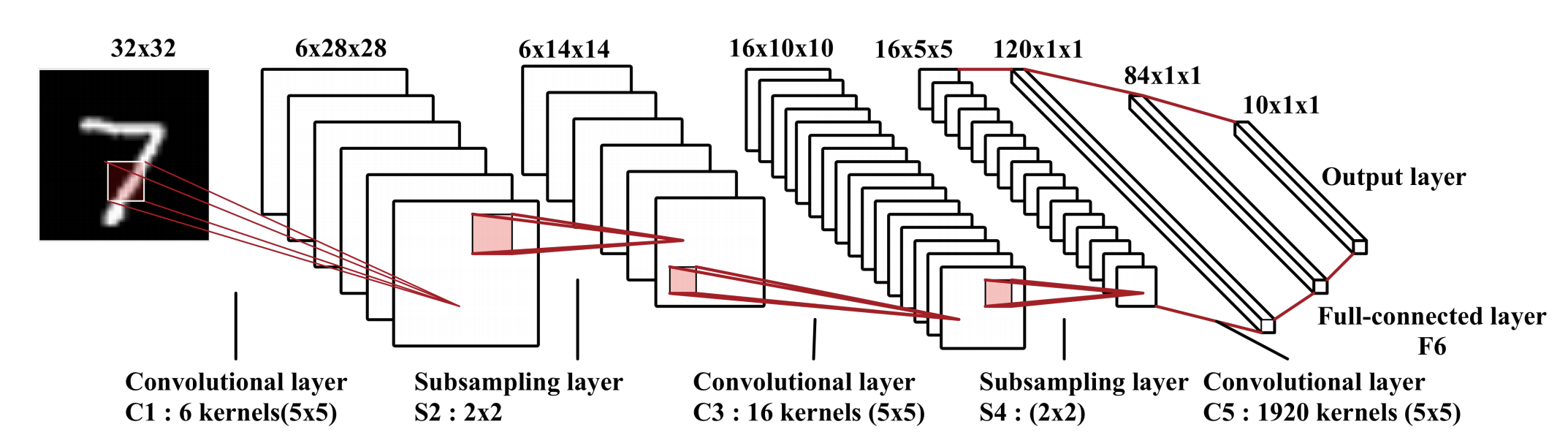
1.卷积层

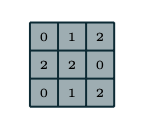
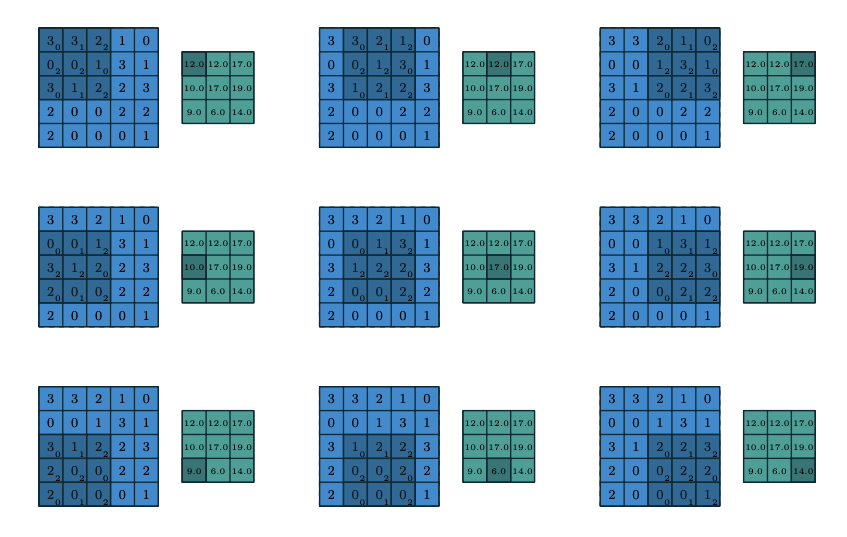
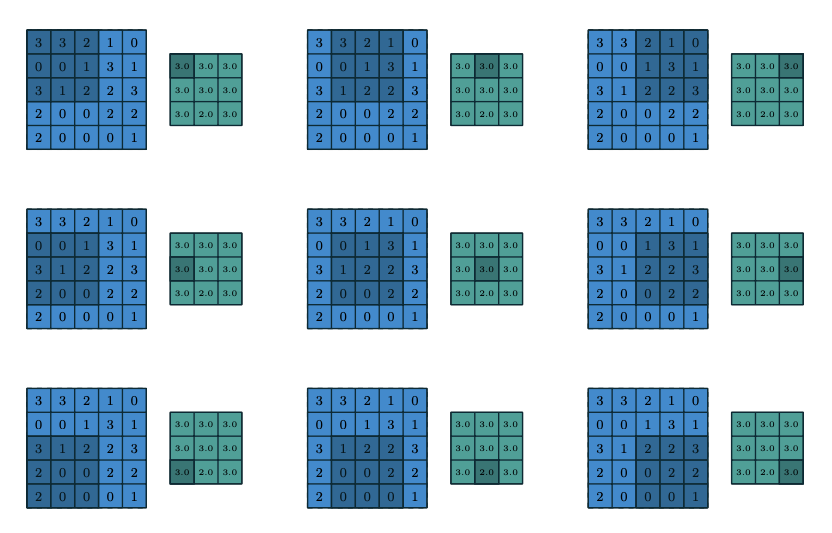
　　卷积层的目的是学习输入的特征表示，如图一所示，卷积层主要由多个卷积核构成，每个卷积核被用于计算不同的特征图。图二给出了卷积计算的一个例子，其中图二(a)为卷积核，图二(b)中蓝色矩阵为输入的特征图，绿色矩阵为利用图二(a)中的卷积核对输入特征图进行卷积计算的结果。输出的矩阵中的每个神经元与输入特征图的局部区域相连，这个局部区域就是当前神经元在上一层的感受野。输出矩阵的计算方式是利用卷积核对每个局部区域进行卷积，即逐元素相乘再相加。在得到卷积结果之后，新的特征图可以通过对每个从局部区域卷积计算得到的神经元应用非线性激活函数得到。这里值得注意的是，同个特征图的生成过程中，输入的多个局部区域共享同个卷积核。最终多个特征图的生成，则是由多个不同的卷积核计算得到。我们把在第l层的第k个特征图中的第(i,j)个位置(这里(i,j)表示第i行第j列)的特征值表示为$z^l_{i,j,k}$，则：

　　其中w表示第l层第k个滤波器的权重，b表示该滤波器对应的偏置项，x表示当前响应值对应的输入块，其中心位置对应特征图中的第(i,j)个位置。这里w为当前特征图中每个特征值所共享。这种权重共享方式具有多种优势，它可以降低模型复杂度，并且可以让网络更加容易训练。在卷积神经网络中引入非线性激活函数，可以让多层网络学习到非线性特征。用 $z^l_{i,j,k}$ 表示非线性激活函数，则卷积特征值的激活值$a^l_{i,j,k}$可以表示为： 经典的激活函数是sigmoid、tanh、ReLU和Leaky ReLU，图三中给出了这四种常见的激活函数。图四中显示了两个卷积层从数字图片7中学习到的特征图，其中左边为第一层卷积层的特征图，大小为6X28X28，右边为第三层卷积层的特征图，大小为16X10X10。从特征图可以看出底层卷积核主要用于学习低层次的信息，如边缘和曲线，而更高层的卷积核则用于学习更加抽象的信息。通过叠加多个卷积层和池化层，我们可以逐渐提取到更加高层次的特征表示。

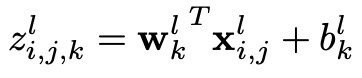
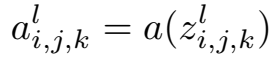
2.池化层

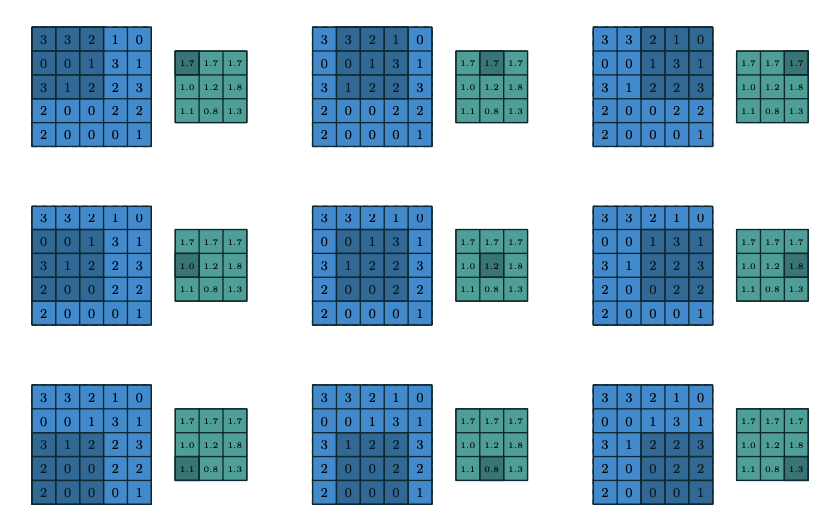
　　池化层通过减少特征图分辨率的方式让网络具有平移和旋转不变性。它经常放在两个卷积层之间。典型的池化操作是平均池化和最大池化。图五给出了池化操作的例子，其中图五(a)为平均池化，图五(b)为最大池化。池化层的每个特征图与它前一层的卷积层对应的特征图相连接。用$pool(.)$表示池化函数，对于卷积层的每个特征图$a^l_{:,:,k}$，对应的池化层的特征值可以表示为：

其中$R_{i,j}$是卷积层特征图中第(i,j)个位置周围的一个局部区域。平均池化取池化区域的平均值，而最大池化则是取池化区域的最大值。

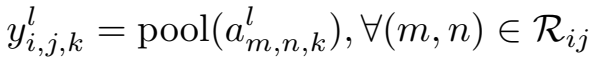
3.全连接层

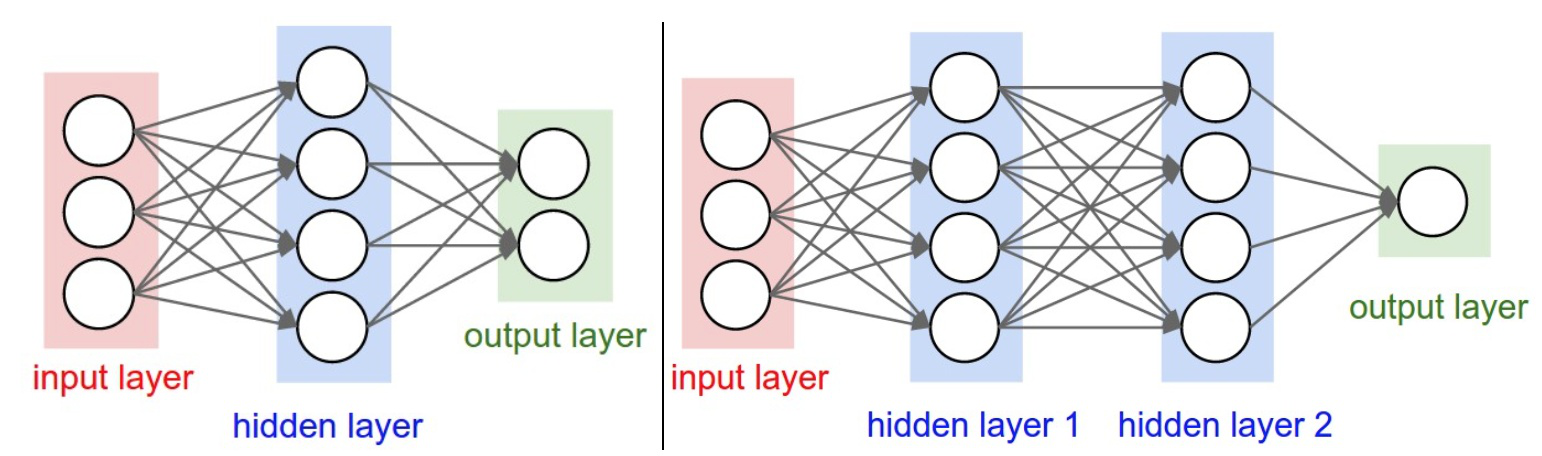
　　在经过多个卷积和池化层之后，可能会连接一个或者多个全连接层来进行高层次的推理。图六给出了全连接层的例子，它们将前一层的所有的神经元作为输入，并将它们与当前层的每个神经元相连接，通过这种方式来生成全局的语义信息。这里的全连接层并不是必须的，它有时候也可以用1X1的卷积层来替代。

4.输出层及损失函数

　　卷积神经网络的最后一层是输出层。对于分类任务，最常用的是softmax操作。另一个比较常用的方法是svm，它可以结合卷积层的特征来处理多种不同的分类任务。用K表示类别数，则其对应的softmax函数可以表示为：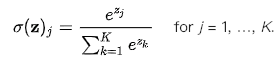

其中$\sigma(z)_j）$表示第j个类别的概率。对于回归任务，输出层一般为普通神经元。
用$\theta$表示所有可学习的参数(比如卷积核的权重和偏置项)，对于具体任务的最优参数，可以通过优化其对应的损失函数来得到。假设我们有N个有标签的训练样本数据，将其表示为{(x(n),y(n))};nЄ{[1,…,N]}，这里x(n)表示第n个输入数据，y(n)是其对应的标签，用o(n)表示卷积神经网络的输出，则其损失函数可以表示为：

对于分类任务，损失函数一般选择交叉熵损失函数；对于回归任务，则一般为均方误差。

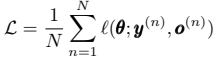
５.反向传播算法

　　训练卷积神经网络是一个全局优化的问题，通过最小化损失函数，我们可以找到最合适的参数集。通常我们采用随机梯度下降方法来优化CNN网络。CNN网络中梯度的计算主要采用了反向传播算法，其中主要利用了链式法则来对不同网络层的权重进行求导。
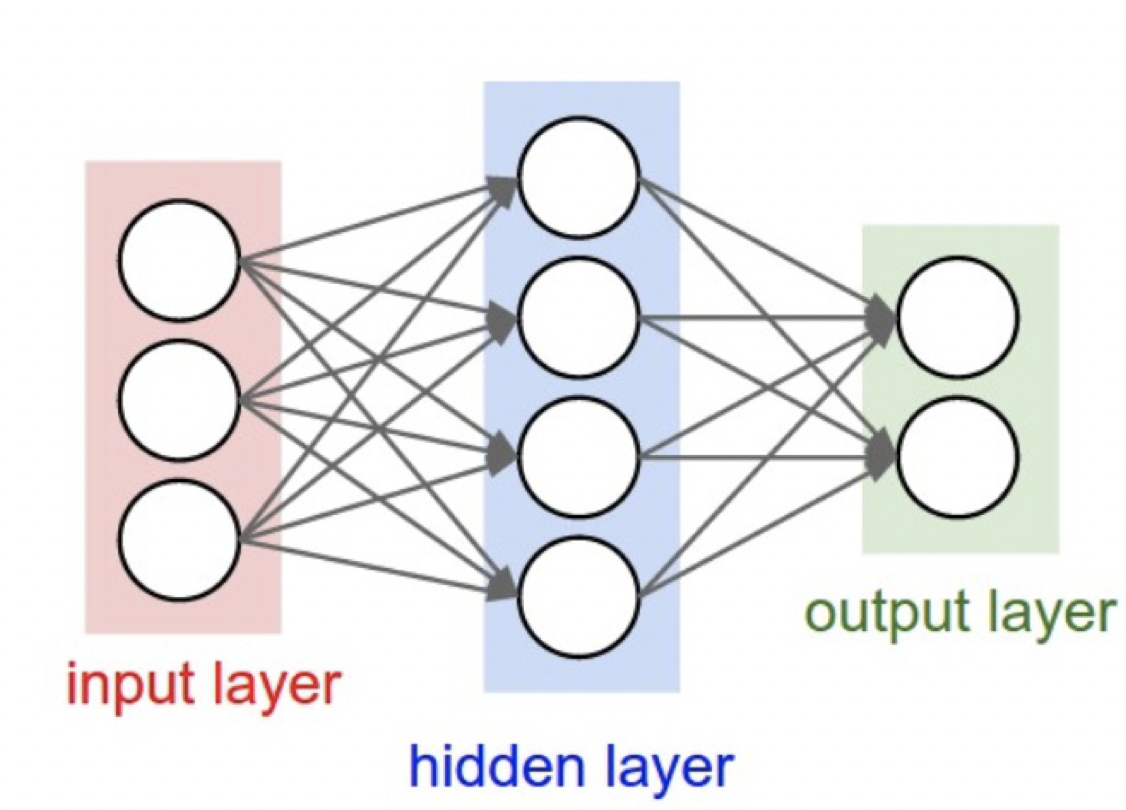
下面给出反向传播的一个简单例子，假设我们的网络结构如图七所示并假设损失函数为
均方误差，则损失函数可以表示为：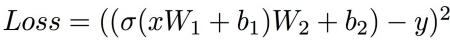

其中x是输入数据，y是其对应的标签；σ为激活函数，这里选取sigmoid函数为激活函数；W1，b1、W2，b2分别为第一层和第二层的权重和偏置项。我们将中间变量定义为：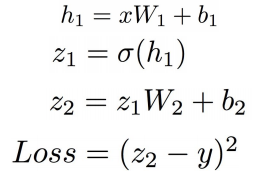

则其前向传播过程如下：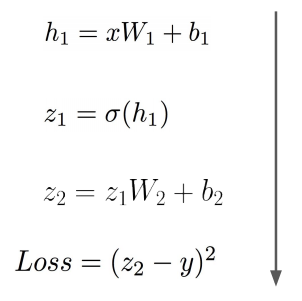

对应的中间变量的梯度即反向传播如下: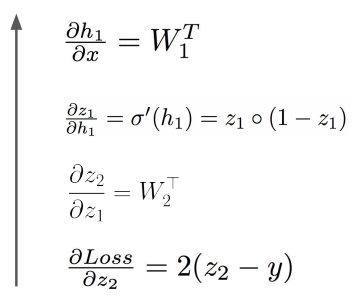

通过链式法则可以很容易计算到各个参数的梯度，如W2和b2的梯度：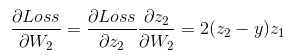

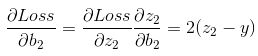
[1] B. B. Le Cun, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, L. D. Jackel, Handwritten digit recognition with a back-propagation network, in: Proceedings of the Advances in Neural Information Processing Systems (NIPS), 1989, pp. 396–404.
[2] Y. LeCun, L. Bottou, Y. Bengio, P. Haffner, Gradient-based learning applied to document recognition, Proceedings of IEEE 86 (11) (1998) 2278–2324.
[3] R. Hecht-Nielsen, Theory of the backpropagation neural network, Neural Networks 1 (Supplement-1) (1988) 445–448.
[4] W. Zhang, K. Itoh, J. Tanida, Y. Ichioka, Parallel distributed processing model with local space-invariant interconnections and its optical architecture, Applied optics 29 (32) (1990) 4790–4797.
[5] X.-X. Niu, C. Y. Suen, A novel hybrid cnn–svm classifier for recognizing handwritten digits, Pattern Recognition 45 (4) (2012) 1318–1325.
[6] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, et al., Imagenet large scale visual recognition challenge, International Journal of Conflict and Violence (IJCV) 115 (3) (2015) 211–252.
[7] K. Simonyan, A. Zisserman, Very deep convolutional networks for large-scale image recognition, in: Proceedings of the International Conference on Learning Representations (ICLR), 2015.
[8] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, A. Rabinovich, Going deeper with convolutions, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015, pp. 1–9.
[9] M. D. Zeiler, R. Fergus, Visualizing and understanding convolutional networks, in: Proceedings of the European Conference on Computer Vision (ECCV), 2014, pp. 818–833.
[10] K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 770–778.

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 524813168@qq.com